Lever's Castle
10. 正则表达式匹配
November 30, 2019
https://leetcode-cn.com/problems/regular-expression-matching/
使用语言:Go
解:
func isMatch(s string, p string) bool {
if s == p {
return true
}
if len(p) == 0 {
return len(s) == 0
}
if len(p) == 1 || string(p[1]) != "*" {
// p 有值而 s 无值的情况返回 false
// p[0] != s[0] 返回 false
if len(s) == 0 || (string(p[0]) != "." && p[0] != s[0]) {
return false
}
// p 长度为 1,则递归传入的 p 为 "", 需要判断 s 是否为空
// p 长度大于 1,但是 p[1] != "*",因此不需要考虑重复匹配的情况,直接进入下一个阶段的匹配
return isMatch(string(s[1:]), string(p[1:]))
}
// p 长度大于 1 并且 p[1] == "*",需要考虑重复匹配的情况
// 如果 p[0] == ".",而已知 p[1] == "*",这是一个万能匹配式,我们只需要知道 p[2:] 是否与 s 中的半段匹配即可。
// 因此,这里靠 i 做驱动,不断地与 p[2:] 做匹配,只要匹配成功,就全部成功,遍历完 i 依然不成功,就返回不成功
// 如果 p[0] != ".",而已知 p[1] == "*",则可以得出 p[0] 对应的字母可以重复任意次。
// 这里 i 从 -1 开始计算的意义在于 x* 可以匹配 0 次或任意多次。从 -1 开始的意思是假设匹配 0 次,则直接将 s 与 p[2:] 进行匹配。匹配如果不成功,就认为应该选择匹配任意多次的分支,则需要保证 p[0] 与 s[i]相等(可以理解为 s[i-1] 已经与 p[0] 想等了,而 s[i:] 又跟 p[2:] 不匹配,这个时候如果 s[i] 还不跟 p[0] 相等,就可以认为完全不匹配了)
// 按照递归的思想,我们只处理子问题,剩下的交给递归去解决
// 这里的子问题是 s[i] 如果跟 p[0] 相等,就继续看 s[i] 后面的元素是否与 p[2:] 匹配即可,一旦后面的元素完全匹配,即可得出 s 和 p 匹配;但是如果不匹配,可能只是因为我们的 s[i:] 还包含了应该跟 p[:2] 匹配的字符,所以继续 i++ 向后检查
sl := len(s)
i := -1
for i < sl && (i < 0 || string(p[0]) == "." || p[0] == s[i]) {
if isMatch(s[(i+1):], p[2:]) {
return true
}
i++
}
return false
}这道题目的难点在于 “” 的处理上。如果没有 “” 我们就只需要考虑 s 和 p 的每个字符是否相等,或者 p 中的某个字符是否为 “.”。
为了规避复杂的 “” 处理,该解法的前半段先处理不带 “” 的情况。
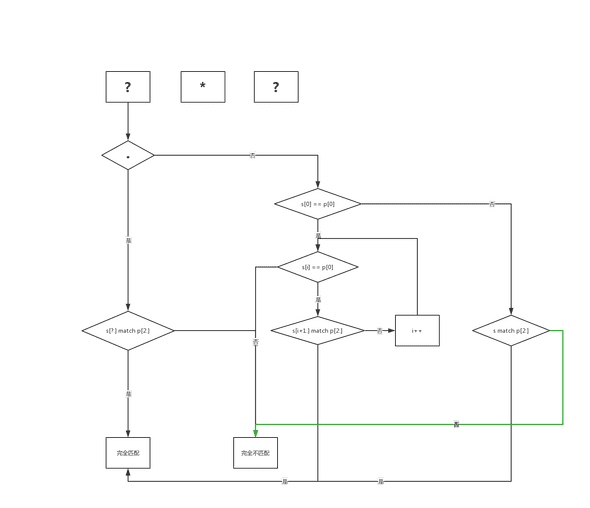
后半段对 “*” 的处理上,实际上是对各种情况的检测,我画了个示意图:
如上图所示,可以划分出这些情况分支:
- p 第一个字符是 “.”
- 1.1. s 中有连续的后半段能够匹配 p[2:],则 s 和 p 完全匹配
- 1.2. s 中没有连续的后半段能够匹配 p[2:],则 s 和 p 不匹配
- p 第一个字符不是 “.”,而 s[0] == p[0]
-
2.1. s 的所有元素中,前 i 个值都等于 p[0]
- 2.1.1. 第 i 个元素之后的某后半段字符串能够与 p[2:] 匹配,则 s 和 p 完全匹配
- 2.1.2. 没有找到满足条件的后半段字符串,则 s 和 p 不匹配
- 2.2. s 的所有元素中,s[i:] 与 p[2:] 不匹配,并且,s[i] != p[0],则 s 和 p 不匹配。(举个例子:s = “aba”, p = “a*a”)
- p 第一个字符不是 “.”,而 s[0] != p[0]
- 3.1. s 与 p[2:] 匹配,则 s 和 p 完全匹配
- 3.2. s 与 p[2:] 不匹配,则 s 和 p 不匹配
根据以上分析,我们发现,实际上在递归的判断匹配的过程中,产生了很多重复路径,为了降低时间复杂度,我们可以引入一个二维数组来缓存已经遍历过的路径结果。
func isMatch(s string, p string) bool {
if s == p {
return true
}
if len(p) == 0 {
return len(s) == 0
}
sl := len(s)
pl := len(p)
mem := make([][]*bool, sl + 1)
for i := range mem {
mem[i] = make([]*bool, pl + 1)
}
return _isMatch(s, p, 0, 0, mem)
}
func _isMatch(s, p string, i, j int, mem [][]*bool) bool {
matched := true
notMatched := false
if j >= len(p) {
return i >= len(s)
}
if mem[i][j] != nil {
return *mem[i][j]
}
var subS string
if i >= len(s) {
subS = ""
} else {
subS = string(s[i:])
}
subP := string(p[j:])
if subS == subP {
mem[i][j] = &matched
return true
}
if len(subP) == 1 || string(subP[1]) != "*" {
if len(subS) == 0 || (string(subP[0]) != "." && subP[0] != subS[0]) {
mem[i][j] = ¬Matched
return false
}
r := _isMatch(s, p, i + 1, j + 1, mem)
mem[i][j] = &r
return r
}
for k:=-1;k<len(subS);k++ {
if k < 0 || string(subP[0]) == "." || subP[0] == subS[k] {
if _isMatch(s, p, i + k + 1, j + 2, mem) {
mem[i][j] = &matched
return true
}
} else {
mem[i][j] = ¬Matched
return false
}
}
mem[i][j] = ¬Matched
return false
}痕迹
没有过去,就没法认定现在的自己